0 はじめに

0.1 自己紹介

こんにちは、Takayukiです。

インターネット上でもほとんど発信せずにひっそりと暮らしている一小市民ですが、上記のとおりしぐまさんからお誘いを頂き、一念発起で筆を取ることにしました。

こういった記事を書いた経験がないため、拙く読みづらい文章も多々あるかと思いますが、何卒ご容赦下さい。

ポーカーに初めて触れたのは約4年前になります。幸運にも知人の知人に数学科出身のプロの方がいたので、ルールを覚えてすぐの段階から初等戦略についてレクチャーしてもらったり、GTO solutionの解釈についてレビューしてもらったり、海外遠征に同行してもらったりと、他のプレイヤーと比べて格段に好条件の入口をくぐることができたと思っています。最初の内は座学で得られた知見を実戦で検証することがモチベーションでしたが、途中から研究一辺倒になり、独学でdocumentationに明け暮れていました。

研究領域を大雑把に表現すると「意思決定過程の明確化」ということになるのですが、個別テーマやキーワードを挙げると、概ね以下のとおりです（本筋ではないため不明瞭なキーワードの羅列のみとなりますがご容赦下さい。）。

• Proactive minESの前段プロセス（観測、選別、拡張）の高度化
• Proactive minESの後段プロセス（正規化、走査）のHeuristics確立
• Passive minES（≠Passive MES）への接続
• HUDの最適化
• 短期繰り返しゲームにおけるアプローチ

なお、2年ほど前から昼夜・休日を問わず仕事に追われがちな立場となってしまったため、その間ポーカーにはほとんど触れられておらず、自身の研究内容も脳内から揮発し始めているような有様です。上記研究のほとんどが道半ばなので着手再開したい気持ちはあるのですが、仕事が落ち着く予定も今のところありませんので、電子の海に埋もれるがまま、定年後の楽しみに取っておくのも一興かなと考え始めているところです。

※仕事絡みの雑談ですが、私の所属する組織ではオンラインカジノのアクセス規制を所管していまして、職場でオンカジやポーカーといった単語が聞き漏れてくると、つい耳がダンボになってしまいます。私自身、先日のCloudflareの大規模障害を契機にCDNの仕組みについて勉強したこともあり、検討会の議論についても興味深く眺めています。

ポーカーの入り込む余地は暫くなさそうです。

0.2 本稿内で使用する表現について

本稿固有の表現や用法がいくつかありますので、以下のとおり示しておきます。

– ゲーム

本稿において取り扱う、ポーカーを抽象化したもの。1.2項及び2.2項で設定するPreflop range、ES、pot、rake、bet size等を前提としたゲームツリーにより規定される二人定和の展開型ゲーム。

– solution

solverによるゲームの解析結果として出力される戦略プロファイル（戦略の組）。本稿ではナッシュ均衡を満たすものと見做す。

– GTO　※狭義

node lockを全く施していない状態で出力されたsolutionに含まれる戦略。

– NLE

一方のプレイヤーの一部の手番についてnode lockを施した状態で出力されたsolutionに含まれる、当該プレイヤーの戦略。node lock equilibrium strategyの略。

– minES

一方のプレイヤー（以下この項目において「Villain」という。）の一部の手番についてnode lockを施した状態で出力されたsolutionに含まれる、もう一方のプレイヤー（以下この項目において「Hero」という。）の戦略。

二人定和ゲームにおいて以下の性質を持つ。

• 上記を満たすVillainの戦略集合に含まれる特定の戦略に対するEVはGTO以上となる。
• HeroがminESを採用する限り、node lockされていないnodeにおいてVillainがどのような戦略を採ろうとも、solutionの示すEVが保証される。

– 役の表現

Str : Straight
2P : Two Pair
TP : Top Pair
PP<TP : Top Pairより弱くMiddle Pairより強いPocket Pair
MP : Middle Pair ※Second Pair
WP : Weak Pair ※Second Pairよりも弱いPair
NMH : No Made Hand ※A high以下
FD : Flush Draw
SD : Straight Draw
CD : Combo Draw ※Pair+FD及びPair+SDを含みます。
◯◯+ : ◯◯以上の全ての役。例えばTP+であればTP以上の全ての役。
◯◯- : ◯◯以下の全ての役。例えばMP-であればMP以下の全ての役。

– nodeの表現

以下の要領で、対象nodeについて ”?” と記載することで表現する。なお、本稿ではPreflopについて基本的に考慮しないため、Preflopの記載は省略する。

（例1）FlopにおけるOOPの最初の手番
　　→　Flop ? node

（例2）Flopにおける、OOP x後のIPの手番
　　→　Flop x? node

（例3）FlopにおいてOOPもIPもxした後の、TurnにおけるOOPの最初の手番
　　→　Flop xx Turn ? node

– 先祖node（群）、子孫node（群）

根（root）でない特定のnode Aの履歴（history）上に存在するいずれかのnode（node Aを除く。）について、node Aの先祖nodeと表現する。また、node Aの全ての先祖nodeの集合について、node Aの先祖node群と表現する。

葉（leaf）でない特定のnode Bから始まる経路（path）上に存在するいずれかのnode（node Bを除く。）について、node Bの子孫nodeと表現する。また、node Bの全ての子孫nodeの集合について、node Bの子孫node群と表現する。

– Flop CB、Turn DB、River TB

Preflop Aggressorによる、Flopのcontinuation betをFlop CB、Turnのcontinuation betをTurn DB、Riverのcontinuation betをRiver TBという。

1 minESの例

1.1 状況設定

本稿では例として、キャッシュゲームを2時間程度打っている中で、特定のVillain（以下単に「Villain」といいます。）について「Turn DBでTP+を100%の頻度で打っている」という確度の高い傾向が見えてきたとして、Villainに対する搾取戦略を考えます。なお、それ以外にはっきりと感知できる傾向はないものとします。

Villainの全てのnodeにおける戦略が完全に推定できるのであれば、それに対する最適反応戦略（MES）を求めれば良いのですが、上記の傾向を基に他のnodeにおける局所戦略の推定を試みたとしても、全てのnodeにおける戦略を完全に推定することは難しそうです。

そこで、既存のsolutionのうち一方に上記の傾向を反映した上で、改めてsolverで解析し、出力された新たなsolutionについて、既存のsolutionからどのような戦略変更が生じているかを確認するアプローチをとることにします。

今回は、以下のシチュエーションにおけるsolverの解析結果を確認していきます。

※筆者がPreflop solverを所持していないため、既に手元に解析結果がある特定のシチュエーションのうちの一つを採用しています。

1.2 solverの設定

solverの設定を考えるに当たり、node lockに関する以下の点について留意します。

※①～③については、今回使用する「GTO+」というsolverの挙動に関する内容となっています。

① node lockは、特定のnodeにおけるrange全体の戦略を固定する機能なので、特定のハンドの戦略のみを固定し、それ以外のハンドの戦略を固定しない状態で解析することはできません。

② 一方のプレイヤーの特定のnodeのみnode lockして解析した場合、solverは、当該nodeの子孫node群だけでなく、先祖node群や先祖nodeから分岐したnode群など、node lockされていない全てのnodeにおいて戦略を変更することで、当該プレイヤーのEVを最大化しようとします。その結果、先祖node群及び先祖nodeから分岐したnode群における当該プレイヤーの戦略が一般的でなくなる（言い換えると、Villainが採っている蓋然性のある戦略の集合から逸脱してしまう）可能性があります。

③ solverは、各ハンドの各アクションについて、コンボ数でなく頻度で管理しています。そのため、特定のnodeのみnode lockして解析した場合、②により先祖node群において戦略変更が生じた結果、当該nodeにおける局所戦略を構成する各ハンドの濃淡が、node lock前後で大きく異なってしまう可能性があります。わかりやすい例として、Flop xbc Turn x? nodeにおいてIPが全てのPP<TPをbetするようnode lockした上で解析をかけると、その先祖nodeであるFlop x? nodeにおいてPP<TPをbetしないように戦略変更してしまい、意図したminESが得られない、といったケースがあります。

④ そもそも、特定のnodeのみrange全体の戦略を精緻に把握できているといったことは、通常ないと考えられます。もしそれができるのであれば、その先祖node群についてもrange全体の戦略を精緻に把握できているはずです。

なお、本稿では、一方のプレイヤーのnode群のみをnode lockし、もう一方のプレイヤーのあらゆるnodeの局所戦略が可変な状態で解析することで、後者の戦略について、solverにProactiveな変更を認めることを基本とします。

（目的に応じて、後者の一部のnode群についてもnode lockした上で解析する手法も考えられますが、本稿では取り扱わないものとします。）

以上を踏まえ、以下の要領でminESを得ることとします。

（以下の設定が最も適切であると主張している訳ではありませんので、アプローチの一つとして受け取っていただければと思います。）

1.3 minESの考察

1.2項で得たsolution Aとsolution Bとで、主要なnodeにおいてどのような差が生じているかを簡単にまとめていきます。

※raiseが絡むnodeなど、遷移確率が決して高くないnodeにおいても非常に趣のある振る舞いが見られるので、幅広く触れたい気持ちはあるのですが、全てのnodeにおけるファクト、解釈の考察、検証等についてフルスペックで書き下すと分量が膨大となってしまうため、私の視点で本稿において最低限触れるべきと考えるnode及び要点に絞ってご紹介します。説明不十分と感じる記述が多々あるかもしれませんが、ご容赦下さい。

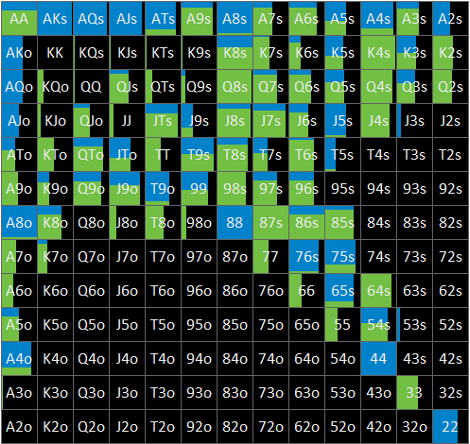
– Flop ? node

Fig. 1-3-1 BB’s strategy @ Flop ? node
(l:GTO r:minES)

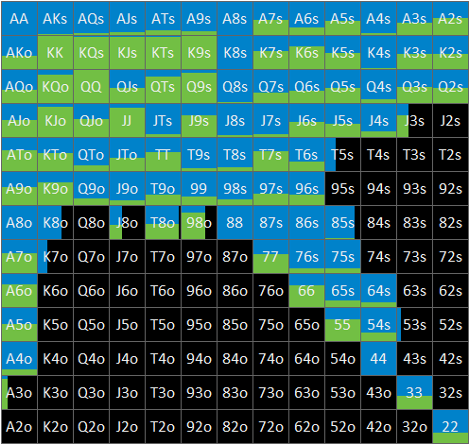
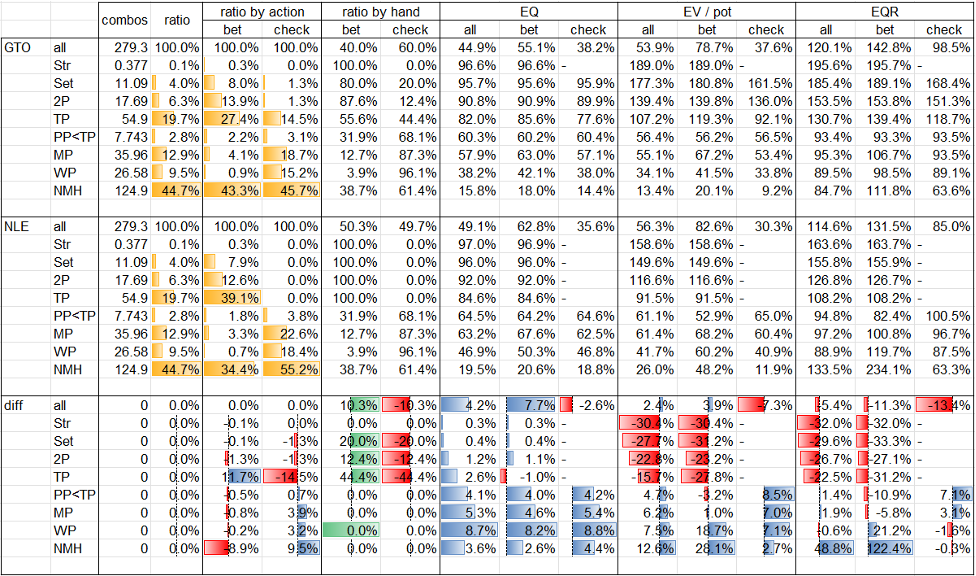
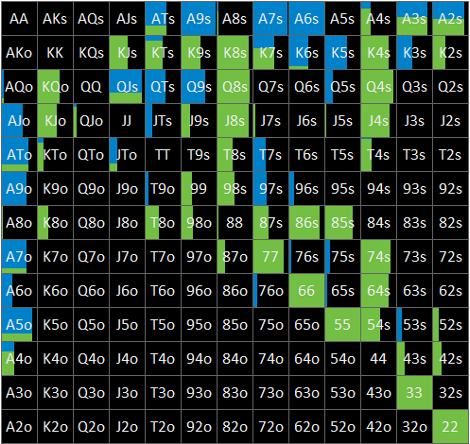
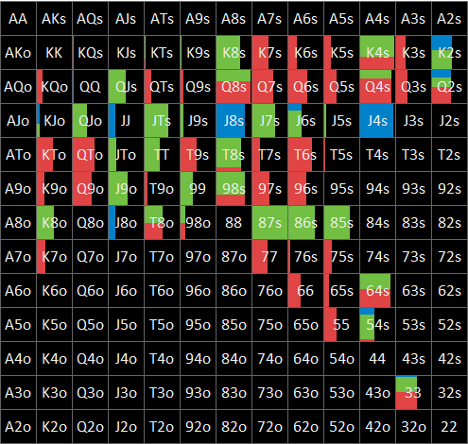
Flop ? nodeにおけるBBの局所戦略はFig. 1-3-1のとおりです。

左側にsolution AによるGTO、右側にsolution BによるminES（BTNの手番においてはNLE）を示しています。青色はbet、緑色はcheckのアクションを表していますが、このnodeでは、GTO、minESともに一面緑のrange checkとなっています。

なお、図からは読み取れませんが、GTOのEVは約37.5% pot、minESのEVは約38.5% potとなっています。

– Flop x? node

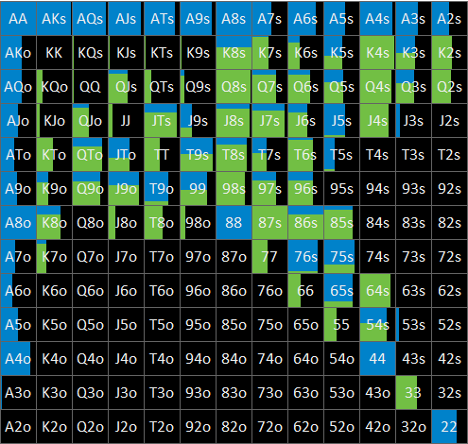
Fig. 1-3-2 BTN’s strategy @ Flop x? node
(l:GTO r:NLE)

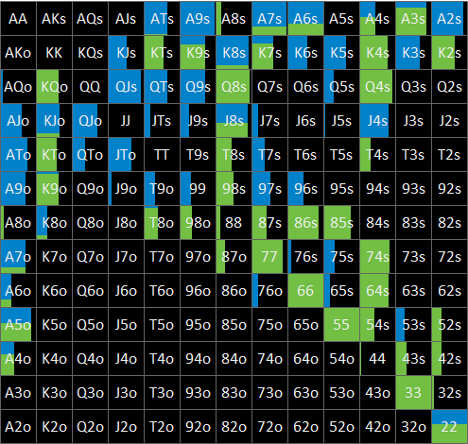
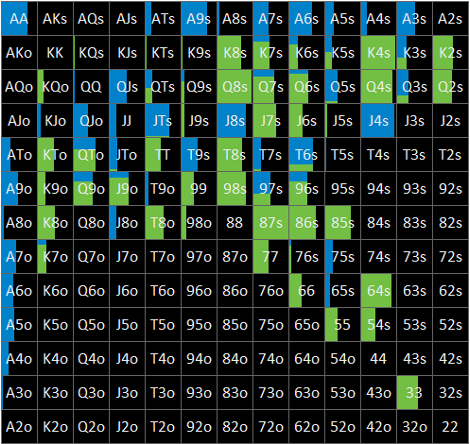
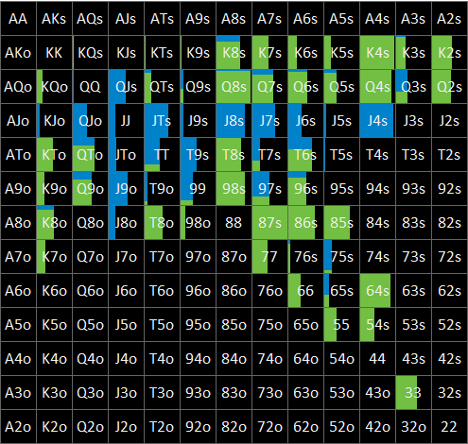
Flop x? nodeにおけるBTNの局所戦略はFig. 1-3-2のとおりです。

1.2項で説明したとおり、solution BはこのnodeにおいてGTOのままnode lockした状態で解析をかけたものであるため、GTOとNLEとで完全に同じ戦略となっています。

なお、図からは読み取れませんが、GTOのEVは約62.5% pot、NLEのEVは約61.5% potとなっています。

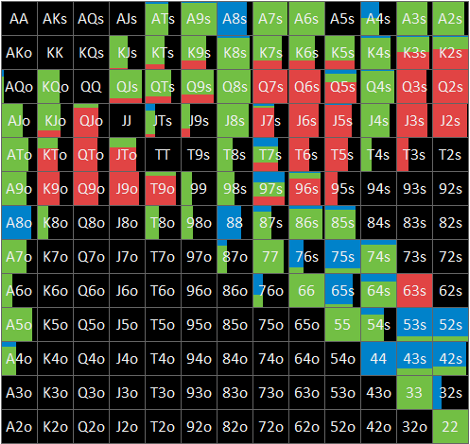
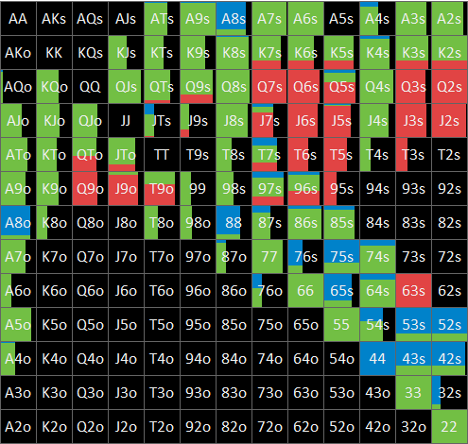
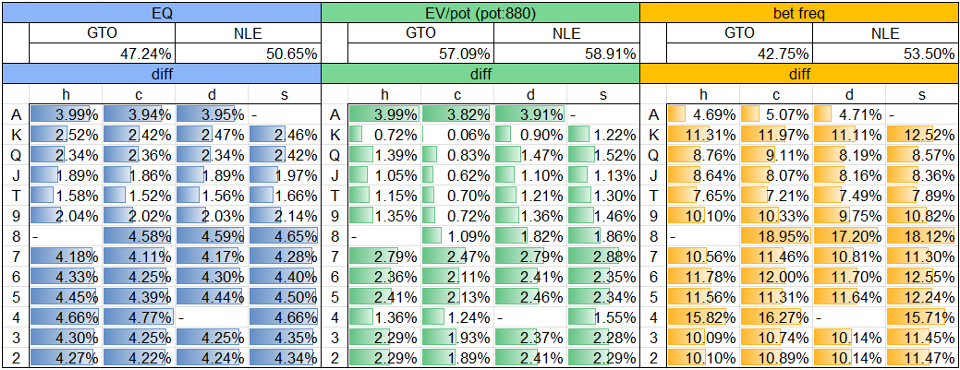
– Flop xb? node

Fig. 1-3-3 BB’s strategy @ Flop xb? node
(l:GTO r:minES)

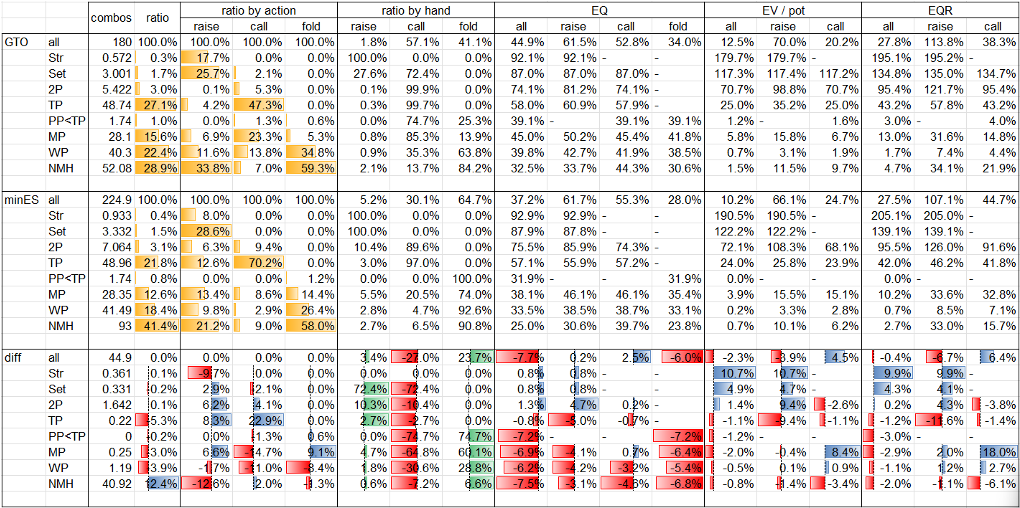
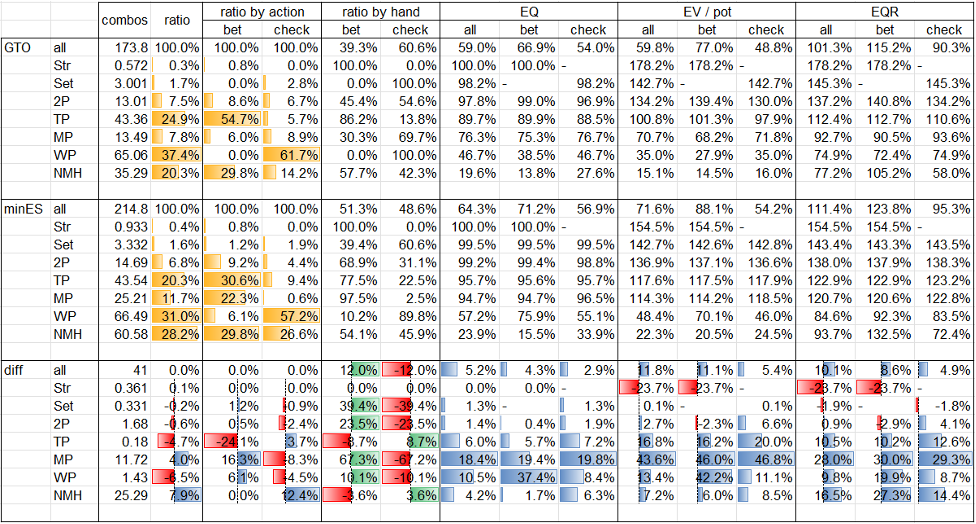
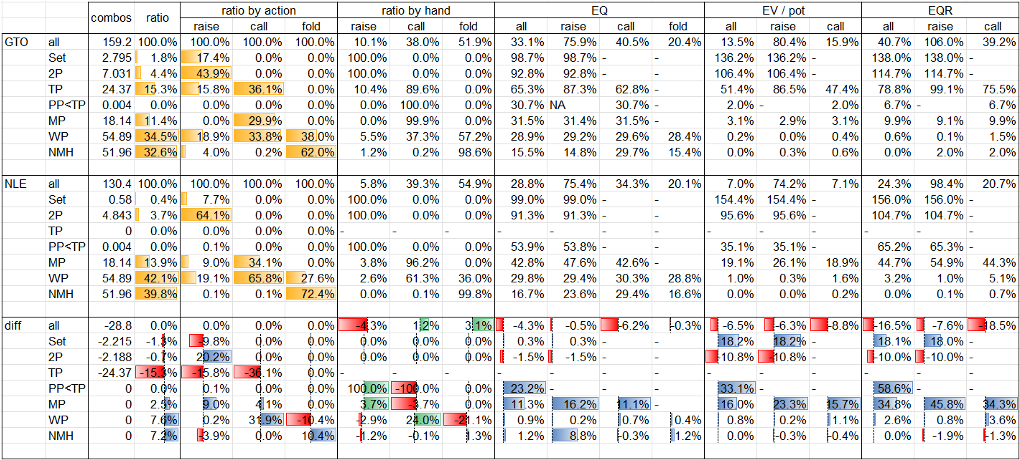
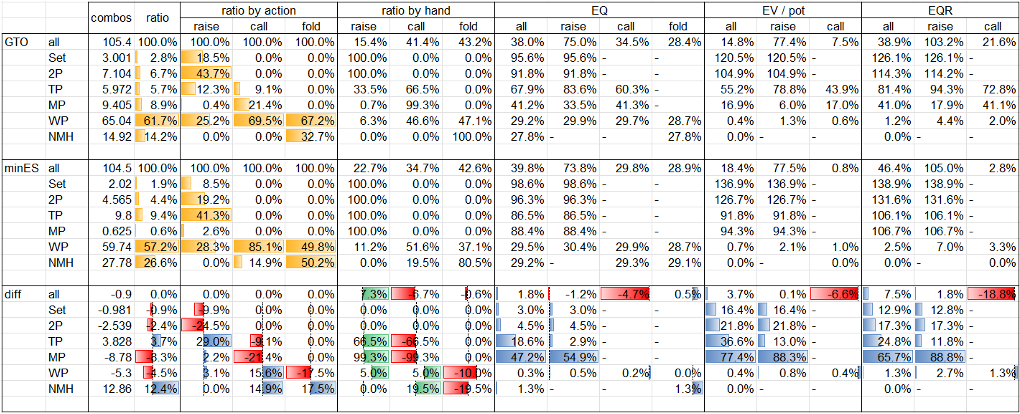
Table. 1-3-3 BB’s data by hand @ Flop xb? node

Flop xb? nodeにおけるBBの局所戦略はFig. 1-3-3のとおり、BBの役ごとのデータはTable. 1-3-3のとおりです。

Fig. 1-3-3について、betやraiseに直面したnodeにおいては、青色がraise、緑色がcall、赤色がfoldのアクションを表しています。

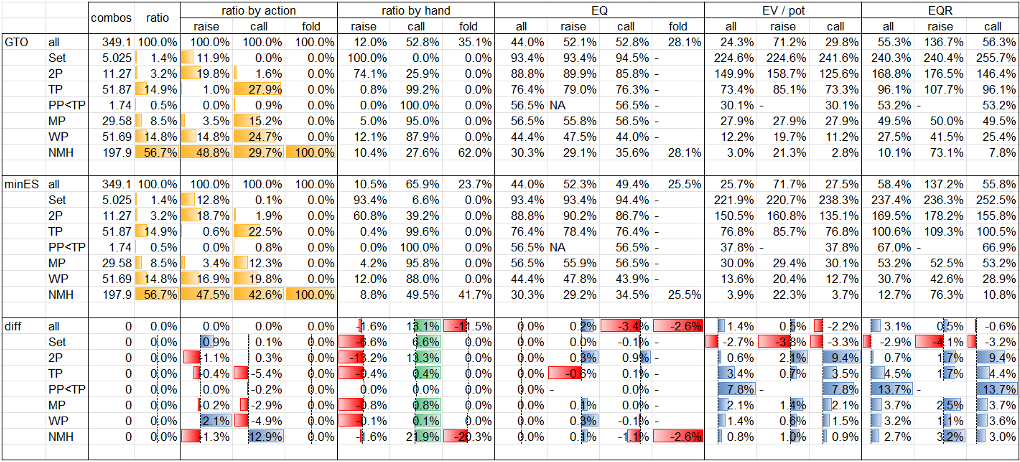
Table. 1-3-3では、GTOとminES（BTNの手番においてはNLE）との役ごとのデータの比較及び差分を示しています。項目としては、左からcombos（コンボ数）、ratio（役比率）、ratio by action（アクションごとの役比率）、ratio by hand（役ごとのアクション比率）、EQ、EV、EQRです。fold EV及びfold EQRは常にゼロなので表示を省略しています。また、以下の3種類のデータバーを用意しています。

• GTO及びminESのratio及びratio by actionの項目について、役の分布を黄色で示しています。
• diff（差分）のratio by handの項目について、役ごとにアクションの分布を緑色（正）又は赤色（負）で示しています。
• diff（差分）のratio by hand以外の項目について、アクションごとに役の分布を青色（正）又は赤色（負）で示しています。

minESの主なポイントは以下のとおりです。

• BBの局所戦略は、GTOからドラスティックに変化している訳ではありませんが、ratio by handを見ると、PP<TPを除くあらゆる役についてGTOよりもcall頻度が高くなっていることがわかります（PP<TPはGTOにおいてもminESにおいても100%頻度のcallで一致。）。range全体のcall頻度は約13ポイント上昇しており、その内数にはGTOにおいてはraiseとなっているSet、2P、SD等の一部（以下「balancer群」といいます。）も含まれていますが、大部分を占めるのは、GTOにおいてはfoldとなっているK-9 highの一部（以下「beneficiary群」といいます。）です。fold rangeのEQを見ると、BTNのrangeはGTOとNLEで全く同一な中で、minESのEQがGTOのEQよりも低くなっていることから、minESでは、GTOのfold rangeに含まれる各ハンドをあまねくcallに変更している訳ではなく、EQが高いハンドを中心にcallに変更していることがわかります。
• minESでは、call頻度を戦略的に上昇させた結果、call EVについては減少した一方で、特にbeneficiary群のEVがゼロから大きく増加したことにより、range全体のEVについては増加しています。このような、solverがGTOから戦略的に頻度を上昇させたアクションのEVが減少するという構造は、minES全般で一部例外を除き幅広く見られるものです。
• 図からは読み取れませんが、beneficiary群の各ハンドのminESにおけるcall EVについて、例えばKcTdは3.2% pot、Kh3hは0.7% pot、QcTcは0.2% pot、JsTcは0.0% potとなっています。これらのハンドのcall EVの組成については、この後、子孫node群における戦略を確認した上でサマライズする際に詳らかにしていきます。

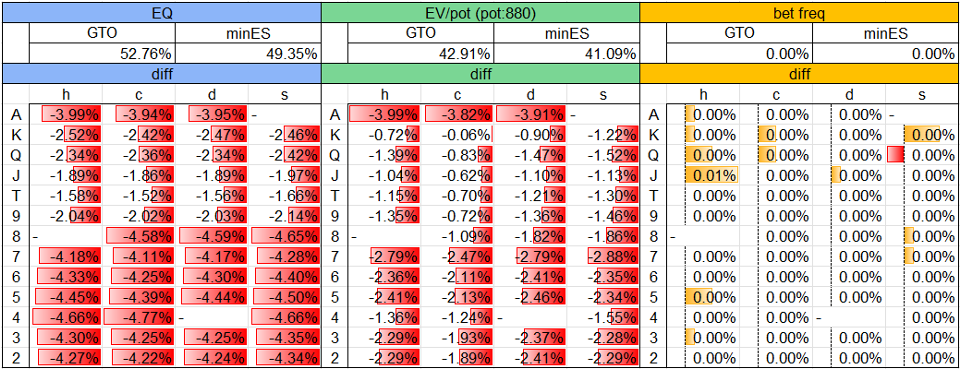
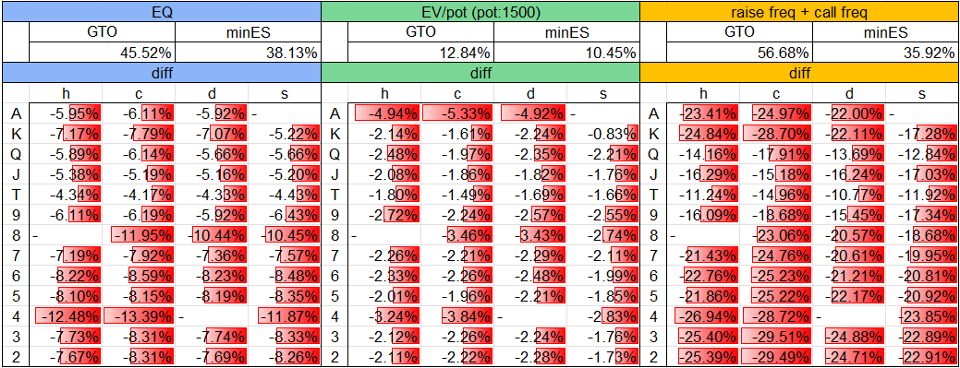
– Flop xbc Turn report

Table. 1-3-4-1 Turn report diffs @ Flop xbc Turn ? node

Table. 1-3-4-2 Turn report diffs @ Flop xbc Turn x? node

Table. 1-3-4-3 Turn report diffs @ Flop xbc Turn xb? node

Turnの各nodeにおけるTurn reportについて、solution Aとsolution Bとの差分はTable. 1-3-4-1～Table. 1-3-4-3のとおりです。

コミュニティカードごとに、EQ、EV/pot、bet頻度（betに直面したnodeにおいてはraise頻度とcall頻度の合計）について、GTOから見たminES（BTNの手番においてはNLE）の差分をまとめています。

主なポイントは以下のとおりです。

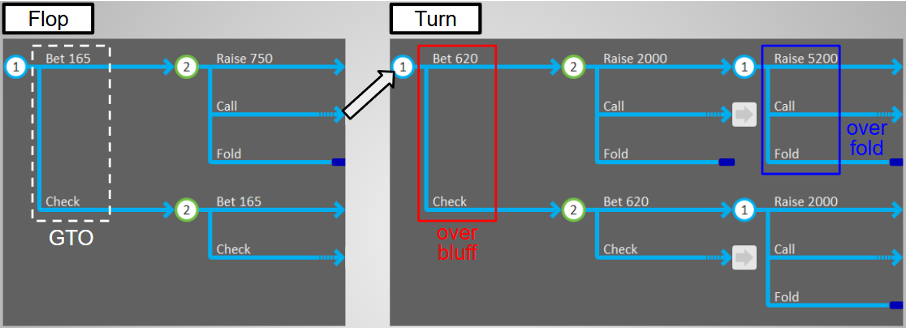
• Flop xbc Turn x? nodeについて、1.2項のStep 3のとおりnode lockしたことで、あらゆるTurnカードにおいてBTNのbet頻度が上昇しています。
• Flop xbc Turn xb？nodeについて、あらゆるTurnカードにおいて、BTNのTurn DBに対するBBのディフェンス頻度が大きく低下しています。ここまでで確認できたsolution Bの振る舞いは、「FlopでBBがGTOよりも広くcallし、TurnでBTNがGTOよりも広くbetし、それに対してBBが広くfoldする」という流れになっており、一見するとBBが自滅しています。
• 図からは読み取れませんが、minESにおけるBBのTurn突入rangeはGTOから変化しているものの、TurnカードごとのEQ等の傾向についてはGTOから大きく変わってはいません。

– Flop xbc Turn 2d ? node

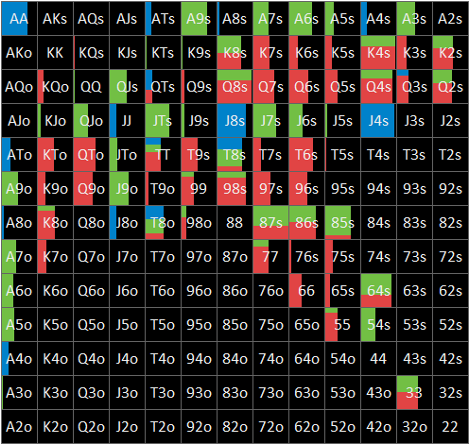
Fig. 1-3-5 BB’s strategy @ Flop xbc Turn 2d ? node
(l:GTO r:minES)

Table. 1-3-5 BB’s data by hand @ Flop xbc Turn 2d ? node

以降、Turnで2dが落ちた場合の各solutionを確認していきます。

Flop xbc Turn 2d ? nodeにおけるBBの局所戦略はFig. 1-3-5のとおり、BBの役ごとのデータはTable. 1-3-5のとおりです。

GTO、minESともにrange checkとなっています。また、minESでは、主にFlop xb? nodeにおいてbeneficiary群をcallに戦略変更したことに起因して、GTOよりもEQが低下しています。

– Flop xbc Turn 2d x? node

Fig. 1-3-6 BTN’s strategy @ Flop xbc Turn 2d x? node
(l:GTO r:NLE)

Table. 1-3-6 BTN’s data by hand @ Flop xbc Turn 2d x? node

Flop xbc Turn 2d x? nodeにおけるBTNの局所戦略はFig. 1-3-6のとおり、BTNの役ごとのデータはTable. 1-3-6のとおりです。

1.2項で説明したとおり、solution BはこのnodeにおいてGTOからTP+を100%の頻度でbetするよう戦略変更した上でnode lockした状態で解析をかけたものであるため、NLEのbet頻度はGTOよりも高くなっています。

NLEの主なポイントは以下のとおりです。

• ratio by actionを見ると、GTOのbet rangeにおけるTP+の割合は49.6%となっているのに対し、NLEのbet rangeにおけるTP+の割合は59.9％となっており、GTOに比してvalue heavyなbetを仕掛けていると言えます。なお、bet rangeのEQが上昇していますが、これはFlop xb? nodeにおけるBBの戦略変更が影響している部分もあります。一方で、bet rangeのうちTPのEQは低下していますが、これは、GTOにおいてはEQの高いTPを中心にbetしていたところ、minESにおいてはEQの低いTPも含め100%の頻度でbetしたことに伴い、bet rangeに含まれるTP全体のEQが落ちたことによるものです。
• bet EVについて、bet range全体で見ると増加していますが、手役ごとに見ると、MP+とWP-とで様相が異なります。後述しますが、BTNのvalue heavyなbetに対し、BBはraise頻度を上げつつfold頻度を大きく上げる応答を示しています。BBのraise頻度の上昇は、BTNの2P+のEVを増加させ、TP-のEVを減少させる方向に働きます。また、BBのfold頻度の上昇は、BTNのTP+のEVを減少させ、WP-のEVを増加させる方向に働きます。BBのraise頻度及びfold頻度の上昇と表裏一体の振る舞いとして、BBのcall rangeや子孫node群の戦略も変化するため、それによるEVの増減もまた影響することになり、これらの重ね合わせの結果　MP+のEVは減少し、WP-のEVは増加しています。それぞれの役について、rangeにおいて占める割合も踏まえてEVの内訳を計算してみると、このnodeにおけるBTNの局所戦略のEVを主として支えているのは、GTOのEV(53.9% pot)についてはTPのbet EV(13.0% pot)及びcheck EV(8.0% pot)である一方で、NLEのEV(56.3% pot)についてはTPのbet EV(17.9% pot)及びNMHのbet EV(8.3% pot)となっており、range全体のEVの内訳におけるNMHのbet EVの比重が大きく増していることがわかります。なお、bet rangeのEQの上昇幅ほどbet EVの増加幅が追随せず、結果としてbet EQRが減少しています。
• check rangeにはTP+が存在せず、それに伴いcheck rangeにおけるNMHの濃度がGTOに比して増しており、EQは低下、EVは減少しています。

– Flop xbc Turn 2d xb? node

Fig. 1-3-7 BB’s strategy @ Flop xbc Turn 2d xb? node
(l:GTO r:minES)

Table. 1-3-7 BB’s data by hand @ Flop xbc Turn 2d xb? node

Flop xbc Turn 2d xb? nodeにおけるBBの局所戦略はFig. 1-3-7のとおり、BBの役ごとのデータはTable. 1-3-7のとおりです。

minESの主なポイントは以下のとおりです。

• BTNのvalue heavyな70% pot sized betに対し、BBはrangeの64.7%をfoldしています。TPはごく一部を除きcallしており、GTOに比して大きな差はありません。一方、MPは8dXdと85s、WPは54sや52sなどのCDに限定してraise又はcallしており、それ以外はfoldしています。また、Set及び2Pはraise頻度が上昇し、その分call頻度が低下しています。結果として、call rangeの70%以上をTPが占めています。
• BTNがTP+を全てbetしているにもかかわらず、BBのcall rangeのEQが上昇しているのは、上記のとおりcall rangeの大部分をTPが占めたことによるものです。なお、BTNは全てのTPをbetしているため、BBのTPはkickerによるEQの差が激しくなっています。例えば、kickerごとにEQを比較すると、以下のとおりです。
  　GTOにおけるAcJhのEQ=60.35% < minESにおけるAcJhのEQ=63.38%
  　GTOにおけるAc6hのEQ=55.64% > minESにおけるAc6hのEQ=51.44%
• balancer群は一部のfoldを除き全体的にraiseしています。これは、BTNのbet頻度が上昇したこと、及び、bet rangeの大半がTPとなったことが一因となって、balancer群について、Flop xb? nodeにおいてraiseせずcallに留め、Turnのx/r頻度の上昇に寄与するインセンティブが働いたと考えられます。なお、Flop xb? nodeでbalancer群をcallに留める要因については、TurnでBTNがcheckした後においても考えられるところで、詳細は後述します。一方、beneficiary群はあまねくfoldしています。
• このnodeでBBがcallした後のRiverの展開について、詳しくは紹介しませんが、軽く触れておきます。River report上、BBのcall rangeのEQ及びEVについては、Table. 1-3-7でもまとめられているとおりminESに軍配が上がります。MPやWPについてはCDに限定してcallしている関係上、そのアウツであるダイヤや3がRiverで落ちた場合はdonk betの頻度がありますが、Riverカード全体の平均で見ると、GTOとminESとで大きな差はありません。一方、BBがcheckした後のBTNのbet頻度について、NLEはGTOよりも平均5ポイント低下しており、これがBBのTurnにおけるcall EV増加に繋がっている要因の一つと考えることができます。Flop xbc Turn xx River x? nodeにおいても似たような構図が見られ、詳細は後述します。

– Flop xbc Turn 2d xx River report

Table. 1-3-8-1 River report diffs @ Flop xbc Turn 2d xx River ? node

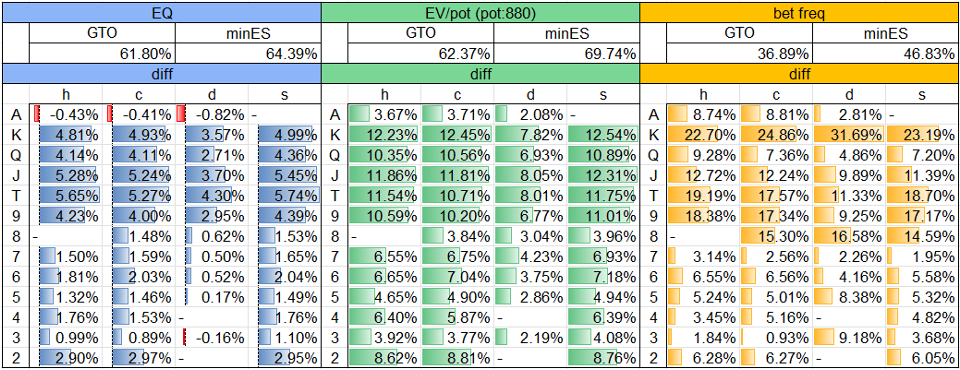
Table. 1-3-8-2 River report diffs @ Flop xbc Turn 2d xx River b? node

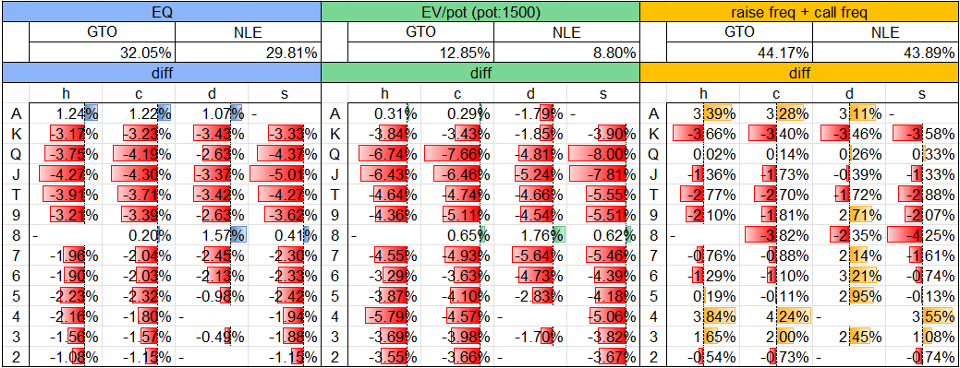
Table. 1-3-8-3 River report diffs @ Flop xbc Turn 2d xx River x? node

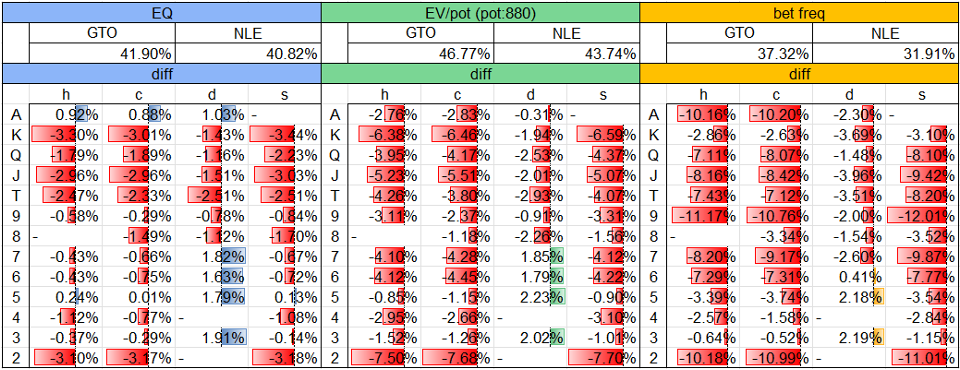
Riverの各nodeにおけるRiver reportについて、solution Aとsolution Bとの差分はTable. 1-3-8-1～Table. 1-3-8-3のとおりです。

主なポイントは以下のとおりです。

• Flop xbc Turn xx River ？ nodeについて、ほぼ全てのRiverカードにおいてBBのEQ、EV、bet頻度がGTOに比して上昇・増加しています。特にK-9が落ちた場合の恩恵が大きく、Flop xb? nodeにおけるbeneficiary群がこのnodeに残っていることによるものと考えられます。
• BBのRiver probe betを受けたBTNについて、GTOに比してディフェンス頻度が若干低下しており、そのEVも減少しています。一方、BBのbet頻度が上昇しているにもかかわらず、BBのcheck rangeはBTNのrangeに対して全く弱まっておらず、それだけが理由という訳ではありませんが、BTNはGTOに比してbet頻度を抑える結果となっています。BTNのbet頻度が落ちるということは、その分だけBBのcheckアクションのEVを奪うことができず、逆に言えば、BBはcheckアクションにおいてEQを実現する方向でEVを増加させていると考えることができます。ここまでで確認できたsolution Bの振る舞いは、「FlopでBBがGTOよりも広くcallし、TurnでBTNがcheckした場合、RiverでBBがGTOよりも広くbetし、BTNはGTOよりも若干広くfoldする一方で、RiverでBBがcheckすると、BTNはGTOよりも広くcheckする」という流れになっており、BTNがTurn DBを打たなかった場合にはBBにとって非常に都合の良い展開になると言えます。この点について、図からは読み取れませんが、BTNがTurn時点でTP+をbet nodeへ手放したことは勿論として、BBがbalancer群をこのnodeに残していることも一定程度寄与していることが別途の検証により分かっています。
• 図からは読み取れませんが、minESにおけるBBのRiver突入rangeやNLEにおけるBTNのRiver突入rangeはGTOから変化しているものの、RiverカードごとのEQ等の傾向についてはGTOから大きく変わってはいません。強いて言えば、Turnに続いてRiverでもダイヤのカードが落ちた場合には、他のカードほどBTNのEVが壊滅的にならないことが挙げられます。これは、Flop xb? nodeにおけるbalancer群にもbeneficiary群にもBDFDがごく少量しか含まれていなかったことによるものと考えられます。

– Flop xbc Turn 2d xx River Jc ? node

Fig. 1-3-9 BB’s strategy @ Flop xbc Turn 2d xx River Jc ? node
(l:GTO r:minES)

Table. 1-3-9 BB’s data by hand @ Flop xbc Turn 2d xx River Jc ? node

以降、RiverでJcが落ちた場合の各solutionを確認していきます。

Flop xbc Turn 2d xx River Jc ? nodeにおけるBBの局所戦略はFig. 1-3-9のとおり、BBの役ごとのデータはTable. 1-3-9のとおりです。

minESの主なポイントは以下のとおりです。

• BBのrange構成として、Flop xb? nodeで広くcallしたbeneficiary群の影響で、MP及びNMHの濃度が増しています。また、BTNがTurn時点でTP+をbet nodeへ手放したことに起因して、BBのrangeのEQが全体的に上昇しており、特にMPとWPの上昇幅が大きくなっています。これらを踏まえてか、BBのbet rangeはGTOから大きく様変わりしており、MPと強いWP（99,K8）で積極的にvalue betし、逆にTPはvalue x/rのためのtrapとしてcheck頻度を上げています。これは、BBがcheckした後のBTNのvalue betについて、GTOであればTPがボリュームゾーンを占めるところ、NLEではBBにTPが存在せずMPがボリュームゾーンを占めることになるため、BBは、BTNのMPをblockしている2PよりもMPをblockしていないTPを優先してvalue x/rに回していると考えられます。また、NMHのEQを見ると、bet rangeよりもcheck rangeの方が高くなっていることから、NMHのうちEQの低いハンドを中心にbetしていることがわかり、実際に戦略を見ると、Q high以下はあまねくbetしていることがわかります。結果として、bet頻度はGTOに比して12ポイント上昇しています。
• Strのbet EVが大きく落ち込んでいるのは、River reportでも触れたとおり、BBのRiver probe betに対し、BTNはGTOに比してraise頻度が低下し、fold頻度が上昇しているためと考えられます。また、range全体のEVは増加していますが、bet EVだけでなくcheck EVも増加しており、その要因として、BBのcheck rangeの大半はWPと強いNMH（K high）であり、それらのEQがGTOに比して上昇していることと、こちらもRiver reportでも触れたとおり、BBがcheckした後のBTNのbet頻度が低下していることが挙げられます。

– Flop xbc Turn 2d xx River Jc b? node

Fig. 1-3-10 BTN’s strategy @ Flop xbc Turn 2d xx River Jc b? node
(l:GTO r:NLE)

Table. 1-3-10 BTN’s data by hand @ Flop xbc Turn 2d xx River Jc b? node

Flop xbc Turn 2d xx River Jc b? nodeにおけるBTNの局所戦略はFig. 1-3-10のとおり、BTNの役ごとのデータはTable. 1-3-10のとおりです。

NLEの主なポイントは以下のとおりです。

• BTNはTurnでTP+を100%の頻度でbetしているものの、RiverにJが落ちたことで、JJがSetに、J8及びJ4が2Pに昇格しています。これらは全て、一部の4X及び2Xと合わせる形でraiseしており、BBのbet rangeの大部分を占めるTP及びMPのEVを奪うことを目的としているものと考えられます。ただし、Turn時点でのSetや2Pがこのnodeに全く残っていないため、raise頻度はGTOに比して低下しています。
• call rangeはほぼほぼMPとWPのみで構成されています。特にMPはBBのbet rangeのうち高EQハンド群をblockしているためbluff catcherとして優秀ですが、WPについても、良いblockerを有しているものを中心に、4Xや2Xも含めてcallしています。
• このnodeでBTNがraiseした後の展開について、詳しくは紹介しませんが、軽く触れておきます。BTNのraiseを受けたBBは、GTOでは8.7%の頻度でraiseするのに対し、minESでは12.2%の頻度でraiseしており、BTNのraise rangeの大半を占めるJ8及びJ4のEVを奪うことで全体のEVが増加しています。また、BTNはAXを持ち得ず、value raise rangeはJJ、J8、J4のみで構成されていることから、BB側はTPよりもMPを優先してbluff catchに回しており、実際、TPよりもMPの方がEQ、EVともに優れています。この構図は、Flop xbc Turn xx River ? nodeにおける、MPで積極的にvalue betを打ち、TPはvalue x/rに回すといったBBの局所戦略と対応しており、BBのRiver突入rangeについて、単なるEQでなくrange構成そのものが圧倒的有利となっていると考えられます。

– Flop xbc Turn 2d xx River Jc x? node

Fig. 1-3-11 BTN’s strategy @ Flop xbc Turn 2d xx River Jc x? node
(l:GTO r:NLE)

Table. 1-3-11 BTN’s data by hand @ Flop xbc Turn 2d xx River Jc x? node

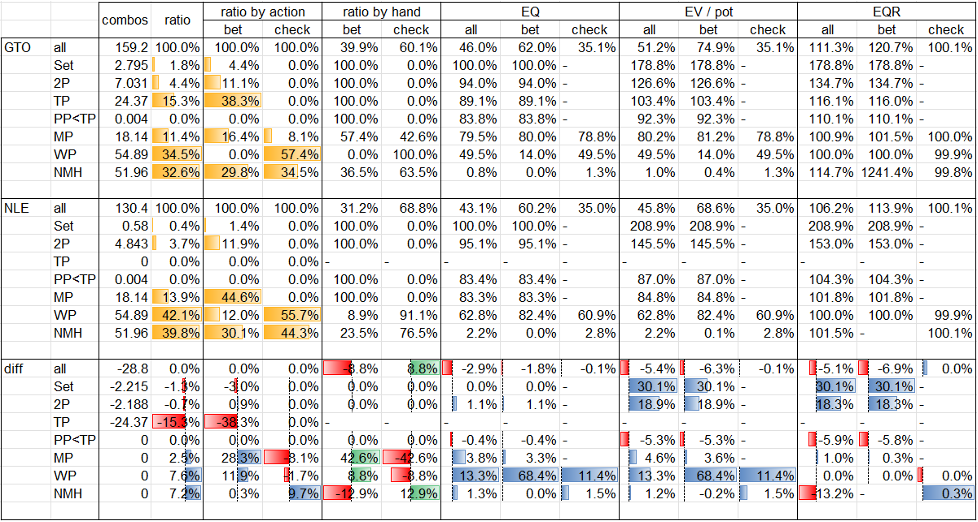
Flop xbc Turn 2d xx River Jc x? nodeにおけるBTNの局所戦略はFig. 1-3-11のとおり、BTNの役ごとのデータはTable. 1-3-11のとおりです。

NLEの主なポイントは以下のとおりです。

• MP+について100%の頻度でbetしているにもかかわらず、bet頻度はGTOに比して減少しています。Flop xbc Turn x? nodeで触れたとおり、このnodeにはTP+が存在せず、それに伴いrangeにおけるNMHの濃度がGTOに比して増している状況ですが、その数多くのNMHについてEQが全くないと承知しながらcheck backすることになります。WPのうちEQが上位のハンドとして、TT（EQ=82.6%）、99（EQ=82.6%）、K8（EQ=81.6%）、Q8（EQ=81.3%）が挙げられ、これらはvalue bet rangeに加えるのに十分なEQを有しているように見えますが、実際にはTTや99にもcheck頻度があり、K8やQ8に至ってはほぼbetしていません。これは、River突入時におけるBBのrangeがBTNのrangeに対して異常に強いためで、仮にBTNが上記のハンドも含めて貪欲にbet頻度を上げようとした場合、BBがcheck rangeにより多くのTP及びそれに対応するNMHを残し、それらによるx/rを仕掛けることで搾取可能となってしまいます。このような、OOPのrangeが異常に強くなったことに伴い、OOPのcheckに対してIPがbet頻度を上げられないといった構図は、GTOにおいても一部のシチュエーションで見受けられる、均衡的な反応の結果と言えます。結果として、BTNはbet頻度をGTOほど上げることが叶わず、BBのbeneficiary群のうち比較的EQが高くcheck rangeに残った大量のK highのEQ実現を許すことになります。
• 詳細は後述しますが、BTNのbetに対し、BBは高頻度でraiseを返します。BTNのbet rangeの大部分を占めるMP及びWPは、BBのraiseに直面すると非常に苦しいですが、かといってbet頻度を下げると、Flop xbc Turn xx River ? nodeにおいてBBが更にbet頻度を上げることを許してしまうため、それを牽制するためにこのbet頻度に落ち着いているものと考えられます。なお、BTNのbetに対するBBのraise rangeの大部分はTPとWPが占めているため、BTNのSet及び2PのEVがGTOに比して大きく増加しています。また、WPのbet EVが更に大きく増加しているのは、GTOにおいてはBBのrangeに対してEQが低いハンドを用いてbluff betしているのに対し、NLEにおいてはBBのrangeに対してEQが高いハンドを用いてvalue betしており、その役割が全く異なるためです。

– Flop xbc Turn 2d xx River Jc xb? node

Fig. 1-3-12 BB’s strategy @ Flop xbc Turn 2d xx River Jc xb? node
(l:GTO r:minES)

Table. 1-3-12 BB’s data by hand @ Flop xbc Turn 2d xx River Jc xb? node

Flop xbc Turn 2d xx River Jc xb? nodeにおけるBBの局所戦略はFig. 1-3-12のとおり、BBの役ごとのデータはTable. 1-3-12のとおりです。

minESの主なポイントは以下のとおりです。

• GTOから戦略が大きく様変わりしています。callについてはWP及びNMHに任せ、MP+は100%の頻度でraiseしています。Flop xbc Turn xx River ? nodeで説明したとおり、minESではTPを優先的にvalue x/rに回しているため、このnodeのraise rangeのほとんどがTPとなっています。ただし、BTNはAXを持ち得ないため、BB側のAXに対応するblockerを有するbluffは用意せず、BB側のSet及び2Pに対応するblocker及びBTN側の2Pに対応するblockerを有するbluffとして8X及び4Xを用いてraiseしています。

– Summary

ここまで、駆け足で端折った内容となってしまいましたが、主要なnodeにおける二つのsolutionの差について見てきました。以下に、solution Bの展開について簡単にまとめてみます。

TurnにおいてBTNがvalue heavyなbetを仕掛けてくることがわかっている場合、BBは、BTNのFlop CBに対し、GTOよりも広くcallします。この広がったcall rangeには、GTOであればraiseしている少量のbalancer群と、GTOであればfoldしている大量のbeneficiary群が含まれています。

これにより、BBのTurn突入rangeは弱まり、実際にBTNのTurn DBに対しては過剰なまでにfoldすることになりますが、raise頻度を上げることで抵抗するとともに、callで耐え抜いたrangeはGTOほどRiver TBを受けずに済むためEVを実現しやすくなります。

TurnでBTNがcheckした場合、BBとBTNとでRiver突入rangeに圧倒的な差が生まれます。RiverではBBのbet頻度が上昇し、BBのRiver probe betに直面したBTNはfold頻度が上昇します。また、RiverでBBがcheckした後のBTNのbet頻度はGTOよりも低下しますが、仮にbetした場合、BBに高頻度でraiseされることになります。

また、Flop xb? nodeにおけるbeneficiary群の各ハンドのcall EVについて、BTNがTurnでbetした場合とcheckした場合とで分割した組成は以下のとおりです。

計算の前提として、BTNのFlop CBのbet sizeは1.650BBです。また、BTNのTurn DB頻度について、GTOでは42.75%、NLEでは53.50%であることがTurn reportからわかっています。

• KcTd
  GTOにおけるcall EV=0.000BB (0.0% pot)
  42.75% × 0.113BB + 57.25% × 2.800BB = 1.650BB + 0.000BB
  minESにおけるcall EV=0.230BB (3.2% pot)
  53.50% × 0.022BB + 46.50% × 4.017BB = 1.650BB + 0.230BB
  →TurnでBTNがcheckした場合のEVが1.217BB増加。
• Kh3h
  GTOにおけるcall EV=0.000BB (0.0% pot)
  42.75% × 0.412BB + 57.25% × 2.574BB = 1.650BB + 0.000BB
  minESにおけるcall EV=0.053BB (0.7% pot)
  53.50% × 0.198BB + 46.50% × 3.435BB = 1.650BB + 0.053BB
  →TurnでBTNがcheckした場合のEVが0.861BB増加。
• QcTc
  GTOにおけるcall EV=0.000BB (0.0% pot)
  42.75% × 0.287BB + 57.25% × 2.654BB = 1.650BB + 0.000BB
  minESにおけるcall EV=0.012BB (0.2% pot)
  53.50% × 0.071BB + 46.50% × 3.500BB = 1.650BB + 0.012BB
  →TurnでBTNがcheckした場合のEVが0.846BB増加。
• JsTc
  GTOにおけるcall EV=0.000BB (0.0% pot)
  42.75% × 0.220BB + 57.25% × 2.731BB = 1.650BB + 0.000BB
  minESにおけるcall EV=0.004BB (0.0% pot)
  53.50% × 0.026BB + 46.50% × 3.527BB = 1.650BB + 0.004BB
  →TurnでBTNがcheckした場合のEVが0.796BB増加。

TurnでBTNがcheckした場合のEVはいずれのハンドでも増加していますが、KTとそれ以外とで大きな差があります。これは、Flopの時点でEQが高いハンドほど、TurnでBTNがcheckした場合にEQを実現しやすいことに起因しています。Riverでのbet頻度を確認すると、全てのTurnカード及びRiverカードの平均で、KcTdは28.8%、QcTcは77.24%と如実に差があり、同じbeneficiary群のハンドであっても、EVの源泉となるnode（端的に言えば役割）が異なる場合があるということがわかります。

なお、Flop xbc Turn x? nodeの子孫nodeにおいて、これまで確認してきたNLEが実戦的に大きな乖離が生じやすいと考えられる場合等には、もう一歩踏み込んで考えることも可能であり、詳細は2.3項で触れます。

2 minESを取り扱う上での注意点

本稿で扱っているminESについて、いくつかの注意点があります。

2.1 Villainの戦略に対してEVが保証されない

HeroがGTOを採る場合、Villainがどのような戦略を採ったとしてもナッシュ均衡時のEVが保証されます。

一方で、HeroがminESを採る場合、Villainに対する「Turn DBでTP+を100%の頻度で打っている」という推定が正しかったとしても、EVが保証されることはありません。

理由は、minESの解析に当たり、Flop xbc Turn x? nodeでTP+以外のハンドの戦略をも固定していること、及び、その先祖nodeでGTOに固定していることから、このminESは、元々想定していたゲームとは異なる（Villainに制約が課されている）抽象化ゲームにおける均衡となっているためです。

例えば、実はVillainのTurn DBにはbluffも大量に含まれており、Turn DB率が高かったといった場合には、minESのEVがGTOのEVを下回ることは想像に難くないと思います。

2.2 程度問題が解決しない

特定の傾向を持つ戦略集合に対するminESを、程度の異なる同一の傾向を持つ戦略集合にぶつけた場合、当該minESの性質が失われてしまい、機能しない可能性があります。

例えば、1項での状況設定におけるvalue heavyは、Turn DBにおいてTP+を100%の頻度で打つというものでしたが、1項から得られたminESについて、Turn DBにおいてTP+を90%の頻度で打つ（ただしGTOで90%を超える頻度で打つハンドについては当該頻度で打つ）傾向のある別の相手に対してそのまま転用した場合、GTOよりも高いEVが得られる保証はありません。

なお、純粋に程度が大きくなった場合に元々のminESが機能しないといった事例は、今のところ確認できていません。

非常にシンプルな例として、以下のトイゲームについて考えます。

上記トイゲームのGTOについては計算して確認することも可能ですが、今回は、solverで解析して得られたsolutionに基づき、一部に限定して簡単に説明します。

Fig. 2-2-1 solution C (l:River ? node r:River b? node)

GTO solutionにおけるRiver ? node及びRiver b? nodeの局所戦略はFig. 2-2-1のとおりです。

OOPは、bet sizeを踏まえAAとQQを2:1の割合で組み合わせてbet rangeを構築しますが、bet頻度を上げすぎるとcheck rangeに残存するQQがAAに比して多くなってしまい、IPのKKとJJを組み合わせたbetによりEVを奪われる損失の方が大きくなってしまうため、IPのKKのEQがちょうどIPにbet頻度が生じる値（約85.7%）となるよう、check rangeにAAを相当量残す戦略を採ります。

また、IPは、OOPのbetに対してraiseする戦略は採らず、KKについては適切な頻度でcallし、JJについては100%の頻度でfoldします。

（OOPがcheckした場合の戦略については割愛します。）

ここで、OOPのbetがover bluffであったと仮定し、それに対するIPのminESを考えます。具体的には、AAのbet頻度はそのままに、QQのbet頻度を若干上昇させ、その状態でnode lockし、改めて解析することでIPのminES Aを得ます。

Fig. 2-2-2 solution D (l:River ? node r:River b? node)

node lockしたsolutionにおけるRiver ? node及びRiver b? nodeの局所戦略はFig. 2-2-2のとおりです。

IPはOOPのbetに対し、KKについては100%の頻度でcallし、またJJについては100%の頻度でfoldします。

IPのKKは、OOPのAAとQQを組み合わせたbetに対するbluff catcherの位置付けなので、OOPのover bluffなbetに対し、KKをcallに寄せる応答は直感的と言えそうです。

（OOPがcheckした場合の戦略もGTOから変化するのですが、やはり割愛します。）

ここで、OOPのbetについて、over bluffの程度を更に大きくしてみます。具体的には、AAのbet頻度はそのままに、QQのbet頻度を更に上昇させ、その状態でnode lockし、改めて解析することでIPの新たなminES Bを得ます。

Fig. 2-2-3 solution E (l:River ? node r:River b? node)

新たにnode lockしたsolutionにおけるRiver ? node及びRiver b? nodeの局所戦略はFig. 2-2-3のとおりです。

IPはOOPのbetに対し、KKについては100%の頻度でraiseし、またJJについては50%の頻度でraiseし、50%の頻度でfoldします。

OOPのbet rangeにおけるQQの割合が一定値を超えたことで、raiseアクションについて、AAに対し更に振り込むリスクを、QQのEVを地に落とすリターンが上回ったということになり、こちらも直感的な応答と言えそうです。

さて、OOPのbetについて、over bluffの程度を大きくした結果、それに対するIPの応答がminES AからminES Bに変化しました。しかしながら、この例では、over bluffの程度が変わったところで、minES AのEVはGTOのEVよりも大きくなるため、over bluffである限りminES Aは機能します。このような、応答が十分直感的と言える範囲の原始的な戦略傾向であれば、その程度が純粋に大きくなったとしても、元々のminESは機能することが多いようです。

一方で、純粋な程度の大小では表現できない場合には、その限りではありません。例えば、同じover bluffであっても、Turnでdrawを全て打つ場合と、TurnでK high以下を全て打つ場合とで、応答の様相が変化するといった事例は比較的わかりやすいかと思います。このような場合には、元々のminESの力学に執着することなく、均衡知識に基づきアドホックに解決を図る必要があろうかと思います。

2.3 多段node lockにおける戦略傾向の適用順序

本稿では取り扱いませんでしたが、複数のnodeにおいて特定の傾向が見受けられる場合（簡単のため、各nodeにおける傾向の確度に差はないものとします。）や、既存のNLEにおける特定のnodeの局所戦略について実戦的に大きな乖離が生じやすいと考えられる場合等には、それに応じて、1.2項で説明したnode lockポリシーを多段階に適用することで、多段node lockを施したminESを得ることが可能です。

なお、特定のnodeに特定の傾向を反映する際、その先祖node群のうち同一プレイヤーの手番についてもnode lockすることを踏まえ、多段node lockを施すに当たっては、Flop ? nodeに近いnodeから順に、node lockと解析を順々に繰り返していくことになります。

例として、以下のSBについて考えます。

Fig. 2-3-1 OOP b-b(ob)/c(of)

このSBは、まずFlop bc Turn ? nodeにおいてover bluffであり、その上で、Flop bc Turn br? nodeにおいてover foldとなっています。

つまり、Flop bc Turn br? nodeにおいては、GTO基準でなく、「Flop bc Turn ? nodeにおいてover bluffであることを踏まえたNLE」を基準としてover foldになっている、ということになります。

よって、SBに対するBBのminESについて、以下の要領で得ることが可能です。

別の例として、今度は以下のSBについて考えます。

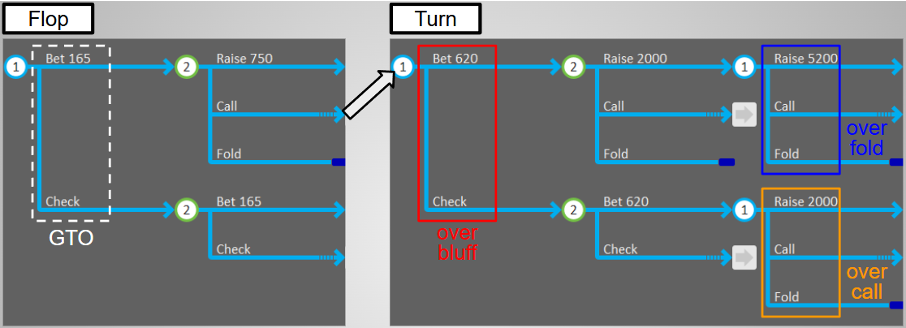
Fig. 2-3-2 OOP b-b(ob)/c(of) + b-x(ob)/c(oc)

このSBは、まずFlop bc Turn ? nodeにおいてover bluffであり、その上で、Flop bc Turn br? nodeにおいてover foldであると同時に、Flop bc Turn xb? nodeにおいてover callとなっています。

ここで、Flop bc Turn br? nodeとFlop bc Turn xb? nodeの一方を優先してポリシーを適用しようとすると、もう一方の傾向の基準が変わってしまうため、solutionが一意に定まらなくなってしまうことに注意が必要です。

つまり、Flop bc Turn br? nodeにおいては、「Flop bc Turn ? nodeにおいてover bluffであることを踏まえたNLE」を基準としてover foldになっていると同時に、Flop bc Turn xb? nodeにおいては、同NLEを基準としてover callになっている、ということになります。

同じNLEを基準として特定の傾向が認められるnodeが複数ある場合には、それらについて同時に戦略変更を施して問題ないと考えられるため、SBに対するBBのminESについて、以下の要領で得ることが可能です（Step 1～4は先程の例と同様です。）。

3 minESの扱い方

2項で触れたとおり、minESには注意点が複数あります。それを踏まえ、我々はminESをどのように取り扱うべきかについて考えたいと思います。

そもそも、目の前に相対しているプレイヤーに対する搾取戦略又はその構築・運用スキームは、何を以って評価・検証されるべきなのでしょうか。

GTO（再三となり恐縮ですが、0.2項で規定した狭義のGTOを指しています。）は、相手の戦略を問わず、一定のEVが保証されています。その意味において、GTOの再現には一定以上の実戦的価値があると言えます。

他方で、minESを含めたGTO以外の戦略は、実際に相手が採りうる戦略の集合（当該戦略に対するMESを含まないものとします。）に対するEV保証を導くことが基本的に困難と考えられるため、そのEVの算出に当たっては、相手の戦略を事前に特定することが必要です。しかしながら、相手がその瞬間どのような戦略を採っているのか、それを正確に確認する術は事実上存在しません（事後に相手とコミュニケーションできたとしても。例えば、bluff catchされた後の「ハンドAでもcallしてた？」「う～ん、ハンドAならcallだけど、ハンドBならfoldしてたかな。」「あ〜、それならbluffせずに諦めるべきだったかぁ〜！」という感想戦は、こと相手の戦略の特定やそれを踏まえた自身の戦略の評価・検証という文脈において、どの程度確からしく意味があると言えるでしょうか？）。そのため、minES又はその構築・運用スキームについて、相手の戦略を以って評価・検証することは困難ということになります。これは即ち、minESの再現の実戦的価値に疑問符が付くことを示唆している、と考えることもできるかもしれません。

※実際のところ、私はminESの再現に一定の実戦的価値が認められる場合があると考えている立場なのですが、話が発散するので割愛します。

ところで、GTO solutionを用いた座学に日々明け暮れている諸兄諸姉においては重々ご承知置きかと思いますが、GTO solutionの分析・類別・解釈等により得られた知見は、GTO solutionの再現に留まらない応用性を有していることがあります。

それはGTO以外のsolutionやそれに含まれる戦略についても同様であり、特に搾取戦略の分析等により得られた知見は、当該搾取戦略の再現のみならず、相手の戦略に蓋然性が生じたと判断した際の戦略構築に活用することが可能です。

その上で、当該蓋然性が、全てのnodeにおける戦略でなく特定のnode群における局所戦略に留まっている場合には、1.3項により得られたminESに関する知見が戦略構築に役立つ場合も多分にあると考えます。

なお、これはminESに限らずGTO等でも同様ですが、上記の戦略構築を見据えた学習に当たっては、一つひとつのハンドやアクションに係るEVが何に起因しているか、その組成をできる限り緻密に分析・理解した上で、戦略構築時のきめ細やかな運用が可能な状態に落とし込む（これは細分化のみを意味せず、むしろ実戦で運用可能なレベルにまで簡素化することを念頭に置いた記述です。ただし、そのリスク評価を入念に行った場合に限ります。）ことが肝要であり、それを怠った場合には、実効的でない戦略が生まれる可能性が高まることを意識するのが望ましいと考えます。

4 ポーカーにおける学習の意義について

折角の機会ですので、3項で記した点も踏まえ、ポーカーにおける学習の意義について、軽く私見を述べておきたいと思います。

巷では「GTOを理解していなければExploitもできない」といった言説をよく見かけますが、私としては完全否定の立場です（今回、GTO solutionをベースとしたminESを扱った手前、誤解を生む可能性があると思い、あえて触れさせていただきました。）。GTOを理解せずとも、Proactive/Reactiveを問わず、Exploitative Strategyを構築することは可能です。

例えば、Riverでover bluffと判断した相手とHUになった際、当該nodeで数多くbluff catchする戦略を採ることや、そこから一定の演繹を経て先祖node群へと考察を遡及させるに至ることは、座学の習慣がなくGTOに馴染みのないプレイヤーにとって、そこまで難しいプロセスとは思いません。

この「Riverでover bluff」の判断を下す拠り所をどこに置くかは、プレイヤーごとに個性が出る重要な部分であり、私としては、GTOはもとより、相手のハンド履歴に限定されるものですらないと考えています。

GTO solutionという一定程度確からしい測距の基準を用いることで、実現可能なExploitabilityの下限に差が出やすいといったことは当然に考えられるため、GTOを拠り所に含めることの意義は認められます。さはさりながら、独り善がりなExploitに振り回されることのないよう、その運用方法や重み付けについては、厳に慎重を期すべきです。「過去にGTO solution上は諦めcheckするハンドでbluffしたのを観測したためover bluffだと判断する」というのは勿論一つの考え方ではあるのですが、その観測事実のみで安直に判断を下してしまうのは、人間という種や相手という個人（あるいはその思考過程や性質）を直視せず、わかりやすい正義の剣に盲目的となっているように感じられます。

他方で、「Riverでover bluffと判断した相手に対してどのような戦略をぶつけることが適切なのか」という問いに対し、その答えを知るためのメルクマールは、GTOやminESを基にした座学から得ることができます。それを様々なシチュエーションや様々な相手を想定して繰り返すことで、共通的な傾向あるいは固有の特徴が見えてくるかもしれません。しかも、その切り口は我々が自由に設定することができ、その結論や粒度は（運用に耐え、且つ、適切な検証を経るのであれば、）我々が自由に調理することが可能です。GTOやminESといった均衡を学習する意義の多くはこの点にあると私は考えます。ポーカーの座学は種々ある中、上記の問いに対する答えを出口に据えて手を動かした結果得られた知見は、書籍や記事から突如与えられ受動的に仕入れた知識よりも真に実効的なものになり得るのではないでしょうか。

（念のため、書籍や記事による学習を否定する主張ではありません。）

トーマス・ヘンリー・ハクスリーによれば、科学は訓練され、組織化された常識以外の何物でもないとのことです。これは、科学という学問は、我々が普段から気軽に用いている方法（事実の観察、比較・分類、推論、検証）を注意深く正確に用いているだけに過ぎず、あくまでも日常生活の延長であるという主張によるものです。その意味において、我々は、目的に沿った正しい工程を踏むことで、ポーカーを科学することができます。本稿は省略している部分があまりに多いため、これを科学と胸を張って称することはいたしませんが、読者のどなたかがポーカーを科学しようと思った際のご参考になれば幸いです。

著者｜Takayuki
直感でポーカーしてます。

• X